Logic: more important than we sometimes think

In a recent discussion between a policymaker and a journalist, an interesting point was raised. The policymaker argued for a vision for the future society and a plan to achieve it. In response, the journalist objected: “Yes, but a vision is so abstract, we now have to make sharp choices.” However, as was rightly pointed out by an expert, Jan Rotmans, this is a false dilemma. A vision actually necessitates making sharp choices—to cease old practices and accelerate new ones. This can be achieved by linking a vision to a strategy and actions, because a vision without action is meaningless, but action without a vision is directionless.

I not only agree with this perspective but also find it to be a brilliant illustration of the importance of logic. Without understanding logic, we are more likely to make the mistake of seeing false dilemmas. With insight into logic, we can prevent such errors more effectively.

Origin of logic

Logic, coming from the Greek word “logoshttps://en.wikipedia.org/wiki/Socrates”, meaning 'reason' or 'word', is an ancient discipline that focuses on the principles of valid reasoning and argumentation. From the early days of philosophical thinking, many great thinkers have helped shape what we now know as logic.

• Socrates (469-399 BC), often considered the father of Western philosophy, played a crucial role in laying the foundations for logical thinking. His method, known as the Socratic method, involves asking a series of questions to lead an interlocutor to a logical conclusion or to expose the inconsistencies in their thinking. This method of critical thinking has contributed greatly to later developments in logic. Rather than writing explicit doctrines of logic, Socrates demonstrated logical reasoning in his conversations, which were recorded by his student Plato.
• Plato (428/427–348/347 BC), a student of Socrates, went further to record and expand his ideas. In his dialogues, Plato used logical structures to explore abstract concepts such as justice, love, and virtue. His 'Theory of Forms' also required keen logical insight to understand the relationship between the physical world and the world of ideas.
• Aristotle (384–322 BC), perhaps the most influential philosopher on the formal structuring of logic, laid the foundations for deductive reasoning in his work “Organon.” He categorized different forms of reasoning, defined terms such as syllogism, and laid the foundation for much of the logic we know today. His systematic approach to reasoning and proof has shaped the discipline of logic for many centuries.

Over the centuries, other cultures and philosophers, such as the medieval Islamic philosophers and later European thinkers, have built on these foundations, leading to the modern logic we know today.

The underestimated importance of logic

Logic is sometimes unfairly pitted against emotion and considered insensitive. It is suggested that too much logic can reduce human quality of life. However, logic is crucial for critically assessing information and making informed choices.

• Imagine a doctor confronted with a mysterious illness. Without logic, this doctor might fall back on superstition or unfounded theories. Logical thinking, on the other hand, allows the doctor to analyze symptoms, make a diagnosis and propose treatment based on scientific knowledge and experience.
• In court, a judge without logic can be influenced by prejudices, personal beliefs, or popular sentiment. But with a logical approach, the judge can objectively evaluate evidence and make a decision that does justice to the facts.
• When making big life decisions, such as buying a home, logical thinking allows us to consider all relevant factors: the home's location, its future value, proximity to amenities, and more.

Logic may sometimes be portrayed as an emotionless approach to life, but it is actually a valuable tool that allows us to make thoughtful, wise decisions. IIn a world lacking logic, impulsivity and randomness would dominate.

What is logic?

Logic helps us think clearly and in a structured manner and determines the validity of our beliefs. It uses premises and conclusions to build arguments. For example, from the premises “All men are mortal” and “Socrates is a man”, we logically conclude that “Socrates is mortal.” However, logic also delves deeper into the relationships between different statements and ideas. Below I describe three forms of logic and two well-known logic tools.

► Types of logic

There are different types of logic, each with their own nuances. Here are examples:

• Propositional logic, also called theorem logic, focuses primarily on statements or propositions that can be considered true or false. Take, for example, the simple statement “It is raining”. This can be either true (yes, it is actually raining) or false (no, it is not raining). Within propositional logic, these basic propositions can be further combined with logical operators such as AND, OR, NOT, and IF… THEN… An example of a combined proposition is: “IF it rains THEN the ground becomes wet”, which indicates that the wetness of the soil is a result of the rain.
• In addition, there is predicate logic, which provides a deeper level of analysis. Rather than focusing on entire statements, predicate logic looks at the individual parts of a statement and the relationships between them. Take the statement “All dogs are mammals”. This highlights two important concepts, “dogs” and “mammals”, and the predicate logic analyzes the relationship between the two, specifically that dogs are a specific group within the broader category of mammals. Within this logic, quantifiers such as “ALL” or “SOME” play a crucial role in describing relationships between objects or groups.
• Finally, we have modal logic. While propositional and predicate logic mainly focus on what is true or false, modal logic looks at the possibilities, necessities, or impossibilities of a particular statement. An example of this is the statement “It COULD rain today,” which does not necessarily state that it will or will not rain, but rather that it is a possibility. In modal logic, 'modal operators' such as CAN, MUST, and MUST NOT are used to indicate degrees of truth or possibility.

► Tools of logic

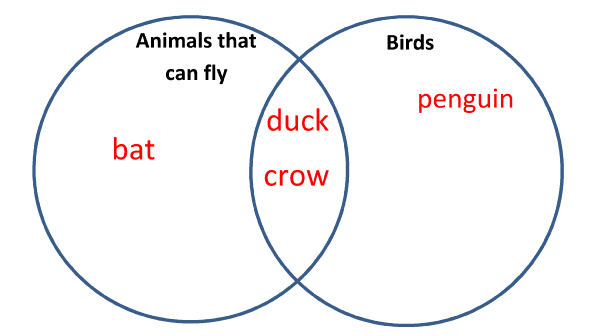
In addition to these types of logic, there are tools of logic such as:

• Venn diagrams: a visual way to understand logical relationships. Named after John Venn, a 19th-century logician, these diagrams illustrate how different groups or sets overlap or not. An example: Take two overlapping circles. One stands for 'animals that can fly' and the other for 'birds'. Where they overlap we find 'birds that can fly'. But we also see unique segments, such as 'animals that fly but are not birds' and 'birds that don't fly'.
• Syllogisms: A form of reasoning from which conclusions are drawn based on two premises. An example: Given “All men are mortal” and “Socrates is a man,” we conclude that “Socrates is mortal.”

The journey through logic is one of discovering structures in our thinking and how we understand the world. These principles, although sometimes abstract, are embedded in our daily decision-making and thought processes.

Limits to logic

While logic is an important tool, there are certainly limits to logic. I discuss some of them below.

► Axioms

Axioms, which come from the Ancient Greek word “ἀξίωμα” meaning “that which is regarded as true,” are the foundations of logical systems. They are unproven, but generally accepted principles. As early as ancient Greece, philosophers such as Euclid used axioms as basic principles. In logic, there are axioms that are considered fundamental truths. Take, for example, the axiom of identity, which states that an object is equal to itself. Or the axiom of non-contradiction: “No statement can be true and false at the same time.” These axioms may sound obvious, but they are crucial. They form the building blocks for more complex reasoning and arguments. In logic, axioms serve as starting points on which further conclusions are based. They are the pillars that ensure the integrity and consistency of our logical thinking.

► Paradoxes

Paradoxes are scenarios that produce logically unresolvable or contradictory results at a deeper level. They confront and challenge the foundations of logic.

1. The Liar Paradox: This paradox revolves around the statement: “I am lying now.” If this statement is true, then the person is lying, which means the statement is false. But if it is untrue, then the person is telling the truth. Here, a direct logical contradiction is presented with no clear resolution.
2. The Barber Paradox: In a village there is only one barber. He shaves everyone who doesn't shave himself, and no one else. But who shaves the barber? Here, a situation is outlined in which the terms of the ruling lead to a logical impasse.
3. The Ship of Theseus: If you have a ship where you gradually replace each piece with a new part, when (if ever) does it stop being the same ship? And if you were to use the removed parts to build a new ship, which ship would be the original? This paradox challenges our concepts of identity and continuity.
4. Russell's paradox: a problem in set theory that arises when considering a set containing all sets that do not contain themselves. The paradox leads to a logical contradiction, challenging the foundations of mathematics.

Although these paradoxes can be confusing, they provide valuable insights into the limits and peculiarities of logical reasoning. They show that there are situations where our usual logical tools fail and we need to consider new ways of thinking.

► The delineated role of logic in assessing truth claims

To assess whether a statement is true, we can look at three aspects:

1. Clarity of Statements: Before we can judge whether a statement is true or false, we must understand what is meant. We cannot judge whether vague or irrefutable statements, involving undefined (or indefinable) concepts, are true or false.
2. Logical consistency: To consider a statement to be true, it is necessary that the statement is logically consistent. If we know that a statement cannot be true because of a logical inconsistency, that is reason enough to reject the statement. If the logical foundation of a statement rests on fallacies, that is a good reason to doubt the truth of the statement. But a logically consistent statement does not necessarily have to be true. Take, for example, a Trump supporter with an anti-Biden banner was interviewed. The man proclaimed that Trump, rather than Biden, would still be president. He then criticized Biden for rising gasoline prices. The interviewer confronted him with the contradiction: how can he blame Biden if he believes Trump is still in power? The man was visibly surprised and did not know what to answer.
3. Available evidence: A logically valid argument is therefore not necessarily sufficient to support a claim. Confirming the accuracy of a claim often requires empirical evidence. For example, a scientific hypothesis may be consistent with logic, but must nevertheless be supported by experimental evidence.

Although logic is indispensable for assessing truth claims, the role of logic is defined. We can only apply logic when there are clear definitions and statements. And after applying logic, it is necessary to look at empirical evidence.

► Emotions and preferences

Individual preferences and tastes are not the result of logical reasoning and do not have to be based on logic. They often arise from a complex interplay of subjective and emotional elements. Logic and emotion are not opponents but complement each other. Both have their own unique value: logic is useful for objective analysis, while emotions provide insights into our personal and social lives. They can also point in the same direction and are therefore both indispensable for a balanced approach to life. When logic and emotion conflict, the situation provides a valuable opportunity for reflection and inquiry.

Illogic: common logical errors

When applying logic, missteps lurk, often known as logical fallacies. These can invalidate our reasoning. Here are four common fallacies with examples:

1. Ad hominem: This does not attack the other person's argument, but his or her character. Example: “I really don't need to listen to your opinion because you are young and inexperienced.”
2. Circular reasoning: This fallacy presupposes in advance what needs to be proven. Example: “God exists because it is stated in the Bible and what it says in the Bible is true because it is the word of God.”
3. Straw man reasoning: This involves misrepresenting or exaggerating the opposing side's argument to make it easier to refute. Example: Person A says, “I think we should invest more money in education.” Person B responds: “So you're saying we should neglect other important sectors like healthcare and infrastructure? That is ridiculous!"
4. False dilemma: This incorrectly represents that there are only two options, when in reality there are several options. Example: Emma indicates that the negative working atmosphere in the team bothers her. Rob responds: “Emma, ​​it's very simple. You have two options: either you stay and stop complaining, or you look for another job.”

These errors in reasoning can lead to wrong conclusions and can also crop up in everyday discussions and debates. Recognizing these fallacies can help us reason better and argue more convincingly.

Conclusion

Logic is crucial for clear reasoning and informed decisions. Despite its usefulness, logic is sometimes considered cold or manipulative, often due to misunderstanding. That is why it is important to include logic in education from an early age. This makes children better equipped to recognize misinformation and weak arguments. In our complex world, this skill is more indispensable than ever.

► To return to the introduction: Rotmans was right. The journalist's suggestion that we do not need vision but sharp choices is a false dilemma. We need both: a vision of the future society and clear choices. Logical, isn't it?